The technique I've chosen for this implementation relies on the RHadoop packages. More specifically, the rmr and rhdfs - the former exposes a MapReduce API, allowing the parallelization of R code execution in a Hadoop cluster, and the latter exposes the HDFS (Hadoop Distributed File System) to the R environment, allowing R to process very large data sets. For examples and discussion of other techniques to scale R, please see here and here.
If you are planning to follow along and run the code, the first thing to do is to have a Hadoop cluster installed and running. There are several ways to accomplish that, depending on your hardware resources and operating system. This is out of the scope of this tutorial, but searching on the internet will give you lots of recipes and one of the simplest ways is to install it in a single-node setup. The second thing you will need is an R environment. As I suggested in part 1 of this tutorial, please take a look at The Comprehensive R Archive Network for instructions on how to install R in your environment. If you have a multi-node Hadoop cluster running, you will have to install R on all the data nodes of your cluster. Finally, the last thing is to install the two RHadoop packages we need for this tutorial: rmr and rhdfs.
Now lets jump into the R code:
Step 1:
The first thing to do is to set two environment variables: HADOOP_CMD and HADOOP_STREAMING according to the corresponding locations of your Hadoop installation. Then you load the RHadoop packages needed to run the code. You can also set the 'backend' property for rmr to be 'local' or 'hadoop'. The interesting thing about setting it to 'local' is that you don't need a Hadoop cluster to test your code. Instead, your code will run in an emulated mode, as if it was being executed in an actual cluster. And you don't need to change anything in your logic.
# set environment variables and load RHadoop libraries
Sys.setenv(HADOOP_CMD='/hadoop-2.3.0/bin/hadoop')
Sys.setenv(HADOOP_STREAMING='/hadoop-2.3.0/share/hadoop/tools/lib/hadoop-streaming-2.3.0.jar')
library('rhdfs')
library('rmr2')
# set the execution mode: 'local' only emulates the MapReduce execution and 'hadoop'
# actually runs the code in the Hadoop cluster
rmr.options(backend = 'local')Step 2:
Here I show you how to upload data from your R environment to the HDFS in the Hadoop cluster. Of course this will not make sense in a real implementation, where usually your data would already be in Hadoop, after landing and being transformed and prepared somehow. Anyway, upon data upload R holds a pointer to the location on HDFS. If no path on HDFS is specified, data is uploaded to a temporary location.
# load input data into HDFS
# you should replace <path-to-file> with the path where you downloaded the input file (german.data-numeric)
hdfs.init()
data <- read.table(<path-to-file>)
data <- to.dfs(data)Step 3:
We need to split our data set into a train and a test set. As a convention to express the y-intercept term, we add a pseudo-feature 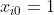 for each example
for each example 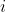 in the data set. We also re-scale the output to be 0 or 1, instead of the original 1 and 2 values, which is necessary for the correct implementation of Logistic Regression. Finally we scale the feature values, so that the optimization algorithm that learns the parameters for each feature may converge faster.
in the data set. We also re-scale the output to be 0 or 1, instead of the original 1 and 2 values, which is necessary for the correct implementation of Logistic Regression. Finally we scale the feature values, so that the optimization algorithm that learns the parameters for each feature may converge faster.
All this transformations can be described by a MapReduce function in R (actually a map-only function in this case), through the rmr package, so that it can leverage the code execution parallelism and data locality in the Hadoop cluster.
All this transformations can be described by a MapReduce function in R (actually a map-only function in this case), through the rmr package, so that it can leverage the code execution parallelism and data locality in the Hadoop cluster.
# split data into train and test sets: first 20% for testing / remaining 80% for training
# add x0=1 to all rows of X (convention)
# scale data to achieve faster convergence
# rescale the output to be 0 or 1 (needed for binary classification using the logistic function)
# instead of 1 or 2
# all this data preprocessing is performed in a distributed fashion
# (when working with enough data) by mappers running in the Hadoop cluster
dataPrep <- function(data,train_size) {
data_train <- mapreduce(
input = data,
map = function(k,v) {
v[,1:(ncol(v)-1)] <- scale(v[,1:(ncol(v)-1)],center=F)
v[,ncol(v)] <- v[,ncol(v)]-1
v <- cbind(1,v)
keyval(k,v[(nrow(v)-train_size+1):nrow(v),])
}
)
data_test <- mapreduce(
input = data,
map = function(k,v) {
v[,1:(ncol(v)-1)] <- scale(v[,1:(ncol(v)-1)],center=F)
v[,ncol(v)] <- v[,ncol(v)]-1
v <- cbind(1,v)
keyval(k,v[1:(nrow(v)-train_size),])
}
)
list(data_train,data_test)
}
Step 4:
Here we actually run the MapReduce function for data preparation that was defined earlier. We also initialize a vector of parameters (theta), and define the hypothesis and gradient functions for the Logistic Regression algorithm.
# prepare test and train datasets (actually, these are pointers to locations in HDFS)
data_prep <- dataPrep(data,800)
data_train <- data_prep[[1]]
data_test <- data_prep[[2]]
# initialize parameters vector theta
theta <- as.matrix(rep(0,25))
# hypothesis function
hypot <- function(z) {
1/(1+exp(-z))
}
# gradient of cost function
gCost <- function(t,X,y) {
1/nrow(X)*(t(X)%*%(hypot(X%*%t)-y))
}
Step 5:
We now define another MapReduce function that runs one iteration of the Batch Gradient Descent algorithm. If we had a very large data set on Hadoop, it would be actually a mini-batch version of Gradient Descent, known as Stochastic Gradient Descent. That is because each mapper would compute a chunk of the input data, yielding a partial gradient, and at the end one reducer would sum all the partial gradients up.
train <- function(theta) {
# runs one step of a batch gradient computation in a subset of the input data defined by the Hadoop cluster
gradient <- mapreduce(
input = data_train,
# compute partial results
map = function(k,v) {
X <- as.matrix(v[,1:25])
y <- as.matrix(v[,26])
p_gradient <- gCost(theta,X,y)
keyval(1,p_gradient)
},
reduce = function(k,v) {
keyval(k,as.matrix(apply(v,1,sum)))
}
)
# output of one MapReduce iteration
values(from.dfs(gradient))
}
Step 6:
Now comes the core of this Logistic Regression implementation, where the algorithm learns the optimization of the cost function through Gradient Descent. It is implemented as a loop for which each iteration computes the gradient of the cost function, updates the parameters vector using the gradient and a predefined learning rate, and checks for convergence according to a predefined tolerance (used to measure if the gradient change is small enough to assume convergence is reached). For this computation, we use the training set previously derived from the entire data set.
# cost function optimization through batch gradient descent (training)
# alpha = learning rate
# steps = iterations of gradient descent
# tol = convergence criteria
# convergence is measured by comparing L2 norm of current gradient and previous one
alpha <- 0.05
tol <- 1e-4
step <- 1
while(T) {
cat("step: ",step,"\n")
p_gradient <- train(theta)
theta <- theta-alpha*p_gradient
gradient <- train(theta)
if(abs(norm(gradient,type="F")-norm(p_gradient,type="F"))<=tol) break
step <- step+1
}
Step 7:
As the last step, we use the learned parameters vector to make predictions using previously unseen examples given by the test set. Those predictions are computed by the logistic function itself, parameterized by the learned vector and using the examples on the test set as input.
# hypothesis testing
# counts the predictions from the test set classified as 'good' and ' bad' credit and
# compares with the actual values
data_test <- as.matrix(values(from.dfs(data_test)))
X_test <- data_test[,1:25]
y_test <- data_test[,26]
y_pred <- hypot(X_test%*%theta)
result <- xor(as.vector(round(y_pred)),as.vector(y_test))
corrects <- length(result[result==F])
wrongs <- length(result[result==T])
cat("\ncorrects: ",corrects,"\n")
cat("wrongs: ",wrongs,"\n")
cat("accuracy: ",corrects/length(y_pred),"\n")
cat("\nCross Tabulation:\n")
print(table(y_test,round(y_pred), dnn=c('y_test','y_pred')))
If your implementation is correct, you should get a result like this:
step: 1
step: 2
step: 3
...
step: 314
corrects: 151
wrongs: 49
accuracy: 0.755
Cross Tabulation:
y_pred
y_test 0 1
0 137 6
1 43 14
The results above mean that the algorithm converged in 314 steps of Gradient Descent and got 75.5% of the test data set correct. That is not so impressive, but better than chance. But if you notice the cross tabulation above, perhaps you see a major flaw. That will be addressed in the next post.
It is important to notice that if you have a very small data set as the one in this example, and you run this code on an actual cluster (setting the parameter 'backend' to 'hadoop'), the overhead of instantiating and submitting MapReduce jobs in the cluster will be way greater than the actual computation resources needed by the algorithm. It would then be unpractical.
Hopefully this small example gave you a rough idea of the great possibilities of RHadoop, and how it can help you avoid the limitations of R running on a single-node machine.
©2014 - Alexandre Vilcek

No comments:
Post a Comment